Preserving information through convolution
- Timofey Uvarov
- Jan 18
- 20 min read
Updated: Apr 29
Bitmap images
Photoshop and other graphics programs generate bitmap images. Bitmaps represent an image using a grid (two-dimensional array). Each cell (pixel) has its own coordinates and color. When editing bitmaps, we work with pixels, not objects or shapes.
Bitmap (raster) images depend on their size (resolution) because they consist of a finite set of pixels. Therefore, bitmaps appear pixelated when zoomed in on the screen or when printed. Bitmaps represent the soft transitions found in photographs and painted images.
Resolution of digital image
Research addresses the problem of changing the resolution of digital images for various classes of images, such as digital photographs, computer-generated graphics, text, etc. The algorithm is based on the principle of maximizing the preservation of image information in the frequency and spatial domains to achieve maximum image clarity and minimum aliasing.
In image rendering, we often see anti-aliasing settings. For example, in 3D Studio Max, in the rendering dialog, you can select many anti-aliasing settings. An ordinary 3D Studio Max user does not want to go into the internal structure of this algorithm but only wants to get the highest-quality image without visible artifacts.
Image resolution is determined by the number of pixels that carry color information. A pixel is a unit of information displayed on a screen. Each pixel reflects a certain amount of information. The more pixels there are in the image, the more detailed the image itself.
Resolution can be represented in different ways:
1. The number of samples (dots) per inch (samples per inch -spi, scanners)
2. The number of dots per inch (Pixels per inch (PPI, monitors)
3. Dots per inch (dpi, printers)
The more dots in the image, the more detail and smoother transitions in images, but the file size also increases with increasing resolution.
It should be understood that the resolution specified in the technical specifications of devices such as printers is a different concept since printers use multiple dots of different colors to print a single dot on an image. In other words, a 600 dpi printer does not mean that it prints 600 dots per inch (600 PPI).
The danger of changing the image resolution is that decreasing or increasing the resolution adds or removes pixels in the image.
Reducing image resolution is called down-sampling, and increasing image size is called up-sampling.

The problems with changing the resolution of images and resampling
Previous research
The main approaches to resizing images are interpolation (linear, bilinear, bicubic), filtering (filters with a separable kernel and an inseparable kernel), and less common ones: fractal scaling, c-spline, etc.
Most users are satisfied with the results of existing resampling tools. Most do not even doubt that the result they get after resampling an image in a program such as Adobe Photoshop can be significantly improved.
We also compared our results with resampling algorithms built into popular software programs.
An overview of popular filters and interpolation algorithms
We have tested the results of many standard resampling filters. Not all of them are suitable for all classes of processed images. The best ones are bicubic interpolation, Lanczos, Mitchell, and Catmull-Rom.
Bicubic interpolation is widely accepted for high-quality resampling. The result after bicubic interpolation is clear, not strongly influenced by step overshoot, and without a “sampling frequency ripple” effect. But anti-aliasing is not enough.
Also, the bicubic method does not work well with fine details in images.
The Lanczos filter is a sinc function multiplied by a weight window with three ripples. Since the second ripple is quite large, the filter produces a large “step overshoot.” The third ripple is the source of a little “ringing.” The main advantages of the Lanczos filter are high image clarity and no aliasing. However, since the spatial characteristics of the filter are far from ideal, the filter cannot be considered universal.
The Mitchell filter has excellent spatial performance and acceptable aliasing, but it generates a rather blurry image; therefore, it cannot be considered universal either.
Catmull-Rom spline is the best of the listed options for day-to-day work. It does a good job of aliasing, the image is sharp enough, and the step overshoot is minimized.
Anti-aliasing and resampling filters in 3DS MAX, Photoshop, ACDSee
3DS MAX
The Kinetix 3D Studio MAX program has a large set of anti-aliasing filters. Anti-aliasing in 3DS MAX is performed by rendering an image with a higher resolution and then down-sampling using the selected filter.

Area — Original filter 3ds max resized.
Blackman — 5x5 filter for sharp images.
Blend — A blend of a harsh filter with a Gaussian filter.
Catmull-Rom is a 5x5 filter that gives good results on boundaries.
Cubic is 5x5 filter based on a cubic spline.
Mitchell-Netravali — A filter that adjusts the balance between blur and ringing.
Quadratic is a 3x3 filter based on a quadratic spline.
Sharp Quadratic — 3x3 filter for sharp edges.
Adobe Photoshop

Bicubic interpolation, Bilinear interpolation, Nearest neighbor method
ACDSee

The popular program ACDSee provides a wide range of algorithms for resampling images.
Rectangular filter
Triangular filter
Bicubic interpolation
Bell
Lanczos filter
Mitchell filter
Resampling algorithm properties.
There are some common artifacts that occur in images being resampled. The quality of the resampling algorithm can be considered the extent to which the possibility of the appearance of any of the unrevealed artifacts in the resulting image is minimized.
Blurring of the Image

Aliasing
This occurs when we try to sample an image with a sampling rate that is too low. The high frequencies of the original image are converted to the low frequencies of the resulting image.

Spatial Frequency Ripple (SFR) occurs when resampling a homogeneous area of an image, which results in an uneven distribution of color in this area.
Ringing (Gibs effect) is an artifact in which the brightness levels near the sharp edges of the original image begin to oscillate in the resulting image.
Step overshoot is a ring with only one oscillation.
Ringing is not always perceived as a negative effect because, with one oscillation, this effect sharpens the edges of the image.

Sub-pixel image shifts occur when the resampling algorithm is implemented incorrectly or inaccurately. After changing the image resolution, the resulting image is shifted compared to the original.
Methods for assessing the quality of resampling algorithms
Strict rules must be followed to assess the quality of resampling filters with different kernels. One popular way is to stretch the image and then downsize it to the original size. Then, you need to compare the resulting image with the original using one of the standard PSNR metrics or another. You can also use metrics that take into account the perception of color by the human eye. All these metrics are very sensitive to the sharpness of the processed image but insensitive to effects such as aliasing or ringing. Therefore, it is necessary to develop unique algorithms to compare the quality of the resampling with filters using different kernels.
One can use Gabor filters to decompose (decompose) an image into perceptual frequencies and compare the two images with weights at each frequency.
Let's compare a reduced and then enlarged image with the original image. It is important to note that quality assessment models perform well only on some subclass of images. For example, a monochrome image, such as text, is not heavily distorted by the step overshoot effect, but images with sharp transitions will be sensitive to ringing effects.

Various resampling algorithms:
1. Original image
2. Down-sampled image image
3. Bicubic interpolation (poor anti-aliasing, torn edges, large overshoot)
4. Lanczos filter (too large ringing and overshoot)
5. Mitchell filter (normal overshoot, but blurry)
6. Catmull-rom filter (blurry),
Objective
Develop a high-quality method of resampling and image processing to achieve maximum quality in accordance with existing metrics and visual perception. Adapt it for the tasks of processing video sequences.
When zoomed out — the most complete preservation of the image information (clarity), the absence of aliasing and other artifacts.
When zoomed in, there is no jigging effect, outliers near sharp edges, and other artifacts, and the image is clear.
DSP approach to resampling and building a resampling filter.
The proposed approach uses the DSP approach to resampling since a raster image can be considered an evenly sifted continuous image.
The criterion of ideal reconstruction is laid down in Nyquest’s theorem. It is expressed in terms of the image spectrum, which means that when we need to build resampling and ani-aliasing filters, we need to pay more attention to the frequency rather than the spatial response of the filter. However, the convolution operation makes it possible for us to connect these areas together and use an already known technique to optimize the filter’s operation.
The proposed algorithm is based on standard signal processing technology. The algorithm allows you to resize the image by a fractional number of times. The standard algorithm has been modified to meet all resampling requirements: border correction has been implemented, and sub-pixel shifts have been eliminated. Polyphase filtering is applied to achieve high performance and computational efficiency. The problem of optimizing the quality of the algorithm’s operation is reduced to the problem of constructing an optimal filter kernel.
Construction of filter
Let us consider the construction of an anti-aliasing filter. The main parameters of the filter are the degree of suppression of unwanted spectral components, the flatness of the frequency and phase characteristics in the pass band and the width of the transition band (between transmission and suppression).
The filter for the resampling task must meet the following requirements: the frequency response must be flat in the pass band, and provide sufficient rejection in the stop band to prevent visible aliasing. Frequencies that are multiples of the sampling frequency must be suppressed particularly strongly to avoid DC aliasing. The phase response of the filter should be linear to prevent asymmetry in the resulting image. The impulse response of the filter should contain as few side lobes as possible, and their amplitude should be as small as possible (to prevent the occurrence of the Gibbs effect).
Unfortunately, all of these criteria cannot be met at the same time.
An ideal low-pass filter is a Sinc function that has many large amplitude side lobes, resulting in ringing. The Gaussian filter kernel (Gaussian kernel), good only in the spatial domain, poorly manifests itself in the frequency domain, which leads to blurring of the image.
Filtering digital data is implemented using the convolution operation with the filter kernel. An ideal low-pass filter has an infinite convolution kernel. One way to approximate an ideal filter is to truncate the infinite convolution kernel to a finite segment. However, this method is bad in that the frequency response of the filter at the same time acquires unwanted ripple (with an amplitude of 9%) near the transition band. Moreover, the amplitude of the pulsations does not change with increasing convolution length. However, the biggest drawback of this filter is how it transforms sudden changes in brightness in the image. After filtering, brightness ripples appear near the boundaries. This makes the filter unusable for graphics.
There are ways to avoid ripple in the filter’s frequency response and to improve the stop band rejection by slightly broadening the transition band. The most common method is the weighting function method. This method involves not truncating the infinite convolution kernel of an ideal filter but multiplying it by a weight function (window) of a special type, which smoothly vanishes outside the specified interval. A lot of weight windows have been invented, they all affect the frequency response of the filter in different ways. We used the Kaiser window because it allows to adjust the trade-off between stop band suppression and transition bandwidth. In addition, it has one of the best characteristics among weight windows.
So, using the Kaiser window, we have built a filter with very good frequency characteristics. However, when we applied it to resampling images, we found that the brightness ripple near the contrast edges did not disappear. Thus, we concluded that when constructing a filter, it is necessary to take into account not only its frequency response but also how it changes the details spatially. When constructing filters for processing an audio signal, only their frequency response is important, since the frequency spectrum of an audio signal is much more important to hearing than a specific waveform. However, for visual perception, it is the spatial domain (specific waveform) that is essential and not the frequency domain. Thus, the task of constructing a good anti-aliasing filter for an image requires a solution taking into account both the frequency and spatial characteristics of the filter. Note that the resulting filter with a Kaiser window would be perfect for anti-aliasing an audio signal.
There are several ways to build a filter to satisfy all resampling requests. One is a window overlay on the sinc function; the other uses linear programming to optimize the frequency and spatial response of the filter. The Remez exchange method is often used to build optimal FIR filters with equal ripple, which are unsuitable for resampling images. Since they do not optimize the impulse response of the filter, which leads to a step overshoot effect, despite its advantages, linear programming is a relatively slow way to optimize filter performance. (it should be borne in mind that we need to carry out the filter construction procedure every time we want to perform the resampling operation since the filter width depends on the compression or stretching ratio of the image). Linear programming helps to minimize the length of the filter kernel, and the length of the filter is not so critical in our case.
In the Impress algorithm, we can independently change 3 main parameters:
Smoothing amount. The Smoothing amount is controlled by the cutoff frequency. Increasing the amount of blur will result in a “blurry” not sharp picture, decreasing the amount of blur will result in a sharp picture, but will also add an aliasing effect.
The suppression in the suppression band is controlled by the width of the Kaiser window. Increasing the parameter results in less aliasing and less SFR; decreasing this parameter will reduce the bandwidth, which will suppress the aliasing effect but increase the SFR effect.
The number of side lobes in the filter kernel determines the trade-off between frequency and spatial characteristics of the filters.
The more spatial ripple, the clearer and alias-free the image we will get at the output, but at the same time, we will increase the ringing effect. The less side ripple in the filter core, the less ringing effect we get.
The suppression of one of the undesirable effects leads to the manifestation of the other. It is necessary to combine these parameters so as to minimize the appearance of each of the artifacts, and to make the filter optimal for the task of changing the image resolution.
A set of parameters that give the correct result, which were selected empirically, are saved in special presets. For example, the “normal” preset is used by default and is currently considered the best for most image classes and results expected from the resampling algorithm. The result of the algorithm’s work with this preset is close in quality to bicubic interpolation but shows comparatively better results in anti-aliasing. The “Sharp” preset emphasizes the sharpness of the image. There are also several presets for dealing with “step overshoot” and “ringing” effects.
Implementation of the Impress
Algorithm The algorithm resamples a one-dimensional signal x [n] of length N into another one-dimensional signal y [n] of length M.
Method
The following steps explain the method used by the algorithm. To increase the speed of the algorithm, some of the optimizations described below can be used.
Choosing the compression/stretching ratio
First, you need to choose the optimal coefficients for the resampling operation. The greatest common divisor K for N and M is found, such that N / K and M / K are greater than 64 (so that the frequency response properties of the resampling filter can be predicted. As a result, the stretch factor is chosen U = M / K, and the compression ratio D = N / K.
Construction of the resampling filter
The resampling filter is a low-pass filter with a cutoff frequency F*min (1/D,1/U), where F is half the sampling frequency. The filter kernel is a sinc function multiplied by the Kaiser weight window. There are several parameters that greatly affect the quality of the filtering.
NLobes is the number of lobes per one side of the filter kernel (may be fractional). If nLobes = 1 then the filter does not create the Gibbs effect near the brightness drops. If nLobes ≤ 2, then a mild Gibbs effect will be observed (one side lobe). If nLobes> 2 then the ringing will be visible to unwanted degree.
SmoothingAmount is responsible for the width of the filter. The wider the filter, the lower the cutoff frequency, and the more blur appears during the filtering process. The narrower the filter, the clearer the image will be at the output. SmoothingAmount is a fractional number that varies in octet 1.
Suppr is the amount of the suppression of the side lobes of the filter (in both impulse and frequency response). This is the β parameter of the Kaiser window. It adjusts the trade-off between the cutoff slope of the frequency response of the filter and the degree of suppression in the notch band. Typical Suppr values are in the region of 2–4.
ES (“ExtraSharpness”) is a parameter that determines the degree of sharpening. The idea of the method is to amplify the frequency response of the high-pass resampling filter in the pass band. To do this, the Gaussian kernel is subtracted from the usual one built by our algorithm.
The main problem with the choice of these parameters is that the result of the filter operation depends on a combination of the choice of these parameters in a very complex, non-linear way.
After choosing the above parameters, the filter is constructed in the spatial domain as follows. The filter width (number of coefficients) is selected as

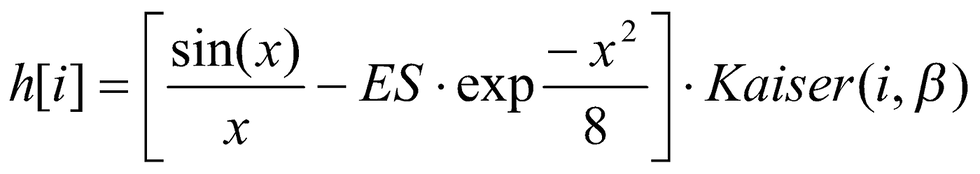

Kaiser window:
![n is a region [-N,N]](https://static.wixstatic.com/media/ecd08f_cc218e7a6c5e462792dc6ff079bab02e~mv2.webp/v1/fill/w_980,h_373,al_c,q_85,usm_0.66_1.00_0.01,enc_avif,quality_auto/ecd08f_cc218e7a6c5e462792dc6ff079bab02e~mv2.webp)
Where I(x) is the Bessel function of the zero-order
Parameter B depends on the suppression requirements of the low-pass filter. Kaiser calculated a simple formula for calculating B and N if known as As (minimum suppression in the suppression band) and delta F (normalized transition bandwidth).





Amplitude-frequency characteristics of filters


Interpolation / Filtering
Decimation To resample the original signal, an interpolation/filtering/decimation sequence is used. First, the original signal is filled with zeros U times. Each original signal value is multiplied by U and then U-1 zeros are written. Before each value of the original signal P = round (U / 2) zeros, and after the last element UP zeros to minimize sub-pixel shifts. The length of the resulting N * U.
The next step is to filter the received signal using the built anti-aliasing filter. Correction at the boundaries at this step is equivalent to copying the boundary values to the left and right beyond the limits of the processing interval.
In conclusion, you need to decimate the received signal by D times. To do this, each D-1 of D values samples from the signal is discarded in a symmetric form (as in interpolation). The length of the received signal is M. The resampling operation is over.
Optimization
The described method produces high-quality resampling when the resampling filter parameters are correctly selected. A huge amount of calculation is unacceptable, for most applications that can draw several optimizations to improve the performance of the algorithm dozens of times without any loss of accuracy-.
Polyphase filtering
Polyphase filtering is a technique that avoids the huge amount of calculations that have to be done during the interpolation process/filtering/approximation to receive the final signal without storing the intermediate signal of long length in memory. Polyphase filtering allows you to express the values of the resulting signal directly through the values of the original signal and the values of the Resampling filter. Using this technique, large values of U and D can be selected without sacrificing the performance of the algorithm. The time spent on the resampling operation depends only on the lengths of the input and output signals and the resampling filter parameters.
Coefficient caching
It is obvious that in the process of resampling images, the operation of one-dimensional resampling is repeated a great many times (for each row and column) with the same parameters. To reduce the number of recalculations, all resampling filter coefficients are stored in memory. This allows for repeated resampling operations, in which all the necessary weights are already prepared in advance in memory.
ExtraSharp Modification (High definition)
A special set of parameters for the high definition filter has been created. For this, a special core and the “Extra sharpness” preset were created.
The idea of the method is to amplify the frequency response of the high-pass resampling filter in the passband. To do this, the Gaussian kernel is subtracted from the usual one built by our algorithm. This results in subtraction of high frequencies.
The formula for obtaining the filter can be written as follows:

Where i = 0, …, L-1, and

ES (“Extra Sharpness”) is a parameter that determines the degree of sharpening increase and can be changed from 0 (original filter) to 0.5 (for maximum sharpness).
Let us illustrate this modification graphically.



As you can see from the diagrams, the new filter has less attenuation in the pass band but good attenuation in the suppression band, which is reflected in better image clarity.
It is important to note that the length of the filter has not increased, and consequently, the time required for filtering has not increased.
Eliminate the Sampling Frequency Ripple effect.
The Sampling Frequency Ripple effect occurs due to the aliasing of the constant component of the signal (DC) during resampling. To prevent it, the suppression of frequencies that are multiples of the cutoff frequency of the filter should be maximized.

When solving this problem, you should vary the parameter values so that they are as close as possible to those obtained in previous experiments and saved settings. Otherwise, we will encounter other artifacts that arise in resampling tasks: the image may be too blurry or have large ripples near the borders.
In previous studies, the authors have struggled with this effect in two ways:
Calculated the filter kernel so that frequencies that are multiples of the sampling rate were analytically assumed to be 0. This approach leads to the use of limited technologies such as cubic splines. The main disadvantage of this approach is that it is very difficult to optimize the filter kernel in the frequency domain, since in the spatial domain we are limited to a narrow class of kernels.
Another method of constructing a filter uses its desired frequency response. This method requires the use of sinc functions and weight windows. The main issue is the choice of the weight window. Unser et al. suggested using 2 weight windows: Dirichlet (rectangular window) and Hanning window. However, the rectangular window has shown poor results in eliminating the SFR effect. The Hanning window eliminates this effect but does not allow for the adjustment of any parameters. Other weighting windows were used in order to further suppress frequencies that are multiples of the sampling frequency, but more suppression in the suppression frequency leads to a wider bandwidth, which makes the image blurry.
Our approach is trying to use the merits of each method.
The resampling algorithm of the “Impress” program is controlled by 3 parameters:
Smoothing Amount — the degree of blurring of the image, which affects the cutoff frequency of the anti-aliasing filter. The higher the Smoothing Amount parameter, the lower the cutoff frequency of the anti-aliasing filter. Changing the Smoothing Amount proportionally “stretches” or “compresses” the frequency axis, and all the lobes in the frequency response of the filter (and most importantly, the minimums of the spectrum) are shifted to the left or right, respectively.
Thus, by changing the Smoothing Amount parameter, we can achieve that at the desired frequency, the filter’s frequency response will be at a minimum. However, at the same time, the minimums of the frequency response may fall on other multiples of the cutoff frequencies we need. It follows that, by changing only the filter's cutoff frequency, it is impossible to achieve minima in the filter's frequency response at frequencies that are multiples of the cutoff frequency.
Another parameter is Ringing Suppression. This parameter affects the width of the frequency response side lobes. So, having fixed the Smoothing Amount parameter at the desired frequency (for example, 1KHz), we can then change the Ringing Suppression parameter until we achieve the fact that at another frequency we need (say, 2x1KHz = 2KHz) there will also be a minimum.
However, it should be added that when changing the Ringing Suppression parameter, one must keep in mind that all parameters have a nontrivial effect on the distribution of the minimums of the filter’s frequency response. The task of eliminating the Sampling Frequency Ripple effect is made easier by the fact that we do not need to provide minima at all multiple frequencies — just a few first multiples of frequencies are enough, since from the construction of the filter it follows that even the maxima of the spectrum ripple at high frequencies will be negligible in their absolute value.
Analytical Rationale
Main Assumption: In the filter kernel, the frequencies that are multiples of the sampling rate should be zero.


The filter built using the Kaiser window uses the parameter B to determine the suppression in the suppression band and the bandwidth. A large value of this parameter gives more suppression in the suppression band, and a less sharp roll-off (wider bandwidth) (Fig. 1). Attenuation of 40 dB means that the aliasing amplitude has decreased by about 100 times.

The Sampling Frequency Ripple elimination algorithm suppresses frequencies that are multiples of the sampling frequency.


Resampling with poly-phase structure
Function PreparePoly()
Function PreparePoly prepares coefficients for a one-dimensional signal resampling operation. The result is stored in three arrays: PMap, LMap, and CMap. The inputs are the length of the original 1D signal, the length of the 1D output, and a filter kernel prepared by the function BuildScaledOPTIMALKernel.
Function DoResampling()
This function directly resamples a 1D digital signal using the PMap, LMap, and CMap arrays prepared by the function PreparePoly. The algorithm can be represented as follows.
To calculate each next value of point [i] of the output signal, you need to calculate the following result: PMap[i] — the value of the point in the original signal, LMap[i] contains the length of the result, the array at the current point (CMapI) contains the LMap[i] coefficients of the result … After the result has been calculated, we save it as a point in the output signal.
Function PreparePoly
Function PreparePoly contains 3 similar, each of which prepares coefficients. The first cycle prepares the coefficients for the left point, for which it is necessary to perform boundary correction (the signal virtually continues by copying beyond the boundaries of the left point). The second cycle is responsible for intermediate points for which no boundary correction is needed. The third loop processes the border on the right.
In each cycle, the corresponding part of the coefficients is PMap, LMap, and CMap, which are calculated and stored for later use in the function DoResampling. Combining these 3 loops into one would be possible, but that would require performing checks on each iteration of such a loop (checking the left and right bounds).
At each iteration (for each point of the output signal), the intermediate results are calculated (the initial index in the original signal, the initial index in the polyphase filter), and we cache the coefficients, going along the filter kernel with a step KU (stretching coefficient).
Detailed description of the polyphase structure
Let X[0, …, Len-1] be the original signal,
KU and KD are the compression ratios and (integers),
Y[0, …, NewLen-1] is the output signal,
Kernel[0, …, KerSize-1] — filter kernel. KerSize must be odd to ensure that the center point is unique.
The interpolation/filtering / decimation approach uses an intermediate array Z[0, …, Len*KU — 1] to store the intermediate signal to be filtered. Let’s look at the direct implementation first.
Direct implementation

Polyphase Implementation


Algorithm explanation
The variable PMapI stores the current index of the array Y, the element of which is to be calculated. Consider the case where PMapI = 1 (calculating the second output pixel). Let KernelSize = 19, KU = 7, KD = 11.
The variable ConvCenter stores the current index in the array Znew, corresponding to the pixel PMapI in the array Y . Here ConvCenter = 16.
Now we need to calculate the dot product of Z[7],…, Z[25] with the kernel Kernel[0],…, Kernel[18]. According to the concept of the polyphase framework, you need to skip zero pixels in the array Z . Dot product must be calculated as follows


Now we can calculate a general expression for SPixel and ConvI

Boundary correction
When the above dot product is considered, the index [SPixel+k] is compared with 0 and with Len. If SPixel+k <0, then put SPixel+k = 0, i.e., duplicate the leftmost pixel beyond the left border. If SPixel + K > Len, then put SPixel+k = Len-1, i.e., duplicate the right pixel.

Examples of the algorithm and comparison
Example 1.

Reducing Image 1 by various algorithms up to a resolution of 200x300.

Then the image was enlarged to 1200x1800 resolution, and the region in which the comparison was made was cropped.


Example 2.
Image for magnification
NEED ORIGNIAL IMAGE



Example 3.
An image with a resolution of 1500x1125 is first reduced, then enlarged by various algorithms. Then the regions in the images are compared.





As you can see from the figures, the Impress: Normal preset gives excellent results for most image classes and presents an excellent compromise for resampling artifacts.
The Extra Sharp and Sharp presets do a great job with sharp images.
Summary
A number of classes in C ++ were developed for working with images using the described methods. In particular, it is the СImageStore class for storing and loading 24-bit and 32-bit images in the Windows system format and a basic set of operations. Also, an interface class CImage was created (containing about 60 functions), encapsulating the functions of the “main” and giving the user ample opportunities for image processing and the programmer — the convenience of expanding the functionality.

The described algorithm is built into the Impress program and is successfully used in practical work with images.
Substantial work has been successfully carried out to optimize the performance of the algorithm. The performance of the algorithm was equal to the performance of other popular algorithms.
Most of the methods for changing the image resolution have been studied.
A set of filters for resampling images has been developed
Work has been done to assess the quality of various resampling algorithms.
A program has been written that implements resampling with the obtained filters.
The algorithm has been tested, and its properties have been shown to be excellent.
Download compiled version of Impress windows application.

